It's our final stop on our tour of the RWS trio: the Writer monad. If you haven't read the previous posts on the State and Reader monads, this post should be understandable even without having read them, though I do recommend going back and reading about them first.
Once again, these posts will be targeted towards people who already have some knowledge about monads, but perhaps are a little fuzzy on specific instances. If you didn't have the Writer monad already implemented for you, how would you go about deriving it from first principles?
Just like the previous posts, this article is designed around you actively working along with the code samples and examples. So make sure you have an editor and REPL handy. Not one for sitting around and listening to long-winded explanations? Itching to get into implementing things? If that's you, here's the skinny version: given the following datatype, implement the Functor, Applicative, and Monad instances for Writer, as well as the listed function signatures.
newtype Writer log a = Writer { runWriter :: (log, a) }
-- The instance heads for the Functor/Applicative/Monad trio,
-- since they're a little different for Writer
instance Functor (Writer log) where ...
instance Monoid log => Applicative (Writer log) where ...
instance Monoid log => Monad (Writer log) where ...
tell :: log -> Writer log ()
censor :: (log -> log) -> Writer log a -> Writer log a
listen :: Writer log a -> Writer log (a, log)For anyone who wants a little more explanation, let's dive into it, shall we?
Let's say we want some kind of trace of our program as it runs, or perhaps we want our functions to be able to log when certain things happen. For the purposes of this post, let's say we're okay with getting all the output once our program finishes running, rather than needing it to be constantly output to a file or stdout.
We could use the State monad to solve this problem, since we've already looked at that. Just have a mutable variable that we constantly update. But for something like a log or trace, we end up writing to the output much more than we end up reading from it, if we read from it at all. So perhaps we can get away with a simpler design if this is all the functionality we need.
How would we go about providing this kind of "write-only global" in Haskell? You know the drill at this point: solve the problem longhand first, see if that results in any obvious boilerplate, then find some way to abstract away that repetition.
Well, if we only need the ability to write things to our log or trace, and don't need a way to read it, it stands to reason that all we need is to add an extra return value to all our functions for them to give back their log messages.
Let's go with log messages as our example; all our functions need to be able to log arbitrary strings alongside returning their "normal" value. So we might end up with something like this:
addTwo :: Int -> ([String], Int)
addTwo x = (["adding 2..."], x + 2)Where if we removed the [String] return from the type, we'd get a function Int -> Int, which is exactly what you'd expect from a function that adds two.1
Arithmetic functions are a bit of a cop-out in example code, but what the functions themselves do isn't particularly important here. Instead, we care that the functions are able to give back some orthogonal information, namely their log messages, and clearly this solves that problem. Now we can use addTwo to create higher-level functions that also log things:
augmentAndStringify :: Int -> Int -> ([String], String)
augmentAndStringify x y =
let (xLog, x') = addTwo x
(yLog, y') = addTwo y
in (["augmenting..."] ++ xLog ++ yLog ++ ["stringifying..."], show (x' + y'))And hey, it works! We're able to accumulate all the log messages that have been output and get our complete set of logs. If we continued writing functions like this, every function in our stack would have log access, and they would be able to log as many messages as they want, including none.
But we're running into similar problems as we had with State, aren't we? The solution isn't very pretty, and we've had to mangle our function definitions quite a bit to keep track of the log messages. We have all the same problems when we need to call other functions: the possibility of accidentally forgetting to use a set of log messages in our final output, of getting them in the wrong order, of typoing and using something twice, and so on. Whatever we can do to improve this, let's do it fast, because this is not a pleasant situation to be in.
Hello monads my old friend. Here we are once again, needing some datatype to implement our monad instances for.
We've been here before. What's the common type that we can factor out from the functions we've written so far? What's the "core type", the "essence" of a write-only accumulator? What's specific to each function, and what's more generally applicable?
addTwo :: Int -> ([String], Int)
augmentAndStringify :: Int -> Int -> ([String], String)You've done this before. I'll let you chew on this for a bit and come back once you're ready.
...
.....
Got a type yet?
If you're looking ahead, you might have come up with the type (log, a), a completely generic tuple, as our core type. And we'll get there. Skip ahead a few sections to the fully-generic Writer if you've already seen how things work in the previous posts.
But for now, we'll roll with the simpler but less flexible type ([String], a) as our core type. Notice that the Int parameters and the String return in our functions above were specific to the functions in question, but the concept of "keeping a log" is orthogonal to what they do.
We've got a type. Let's put it inside a data definition and give it a shot. Since we're not all the way to the fully general solution, we'll call this one a Logger.
data Logger a = Logger { runLogger :: ([String], a) }Again, we don't technically know whether this will form a valid monad just by looking at it. All we can do is give it a shot, try to write the instances, and see if what we end up with obeys the monad laws.
But before we dive into implementing, why would doing this transformation and rewriting all our functions to use this datatype even help us in the first place?
Recall the functions that a monad gives you: return (or pure), and (>>=). Look at their abstract types:
return :: Monad m => a -> m a
(>>=) :: Monad m => m a -> (a -> m b) -> m bHow do the types of these functions relate to our actual datatype?
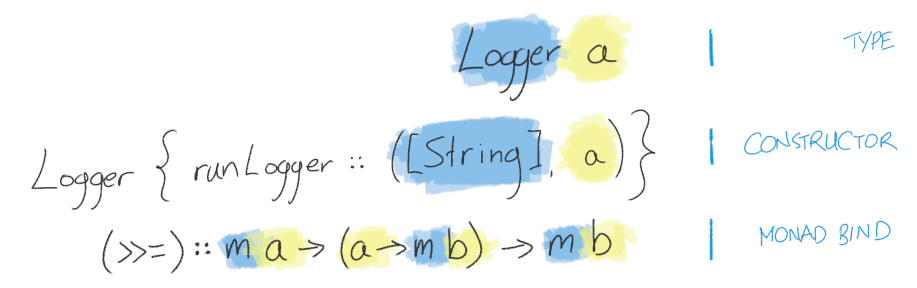
Our log accumulator has been abstracted away underneath the m type parameter in (>>=); as we wanted, we no longer have to worry about keeping track of the accumulator ourselves. The only thing we have access to, is the "normal return value" of any functions we call. If we construct our functions using (>>=), the boilerplate of constructing our final log output should disappear.
So assuming we correctly implement (>>=) and our functor/applicative/monad instances to do that parameter passing for us, we might end up with something like this:
addTwo :: Int -> Logger Int
addTwo x = Logger (["adding two..."], x + 2)
augmentAndStringify :: Int -> Int -> Logger String
augmentAndStringify x y =
Logger (["augmenting..."], ()) >>= (\_ ->
addTwo x >>= (\x' ->
addTwo y >>= (\y' ->
Logger (["stringifying..."], show (x' + y')))))Which definitely looks a little weird, but overall, it's not that bad! There's some funkiness with the first "augmenting..." messsage, since we need to maintain the correct order, but overall what we got isn't that dissimilar from a "normal" implementation. And crucially, we never have to manually construct the final log output anywhere or keep track of the log outputs from the functions we call; that part has been abstracted away. (>>=) is now the one responsible for keeping track of log outputs and assembling it all together. So whatever implementation we write for monadic bind, that’s where we move the log construction that previously we were doing manually.
Exercise 1: Implement the Functor, Applicative, and Monad instances for our newly-defined Logger type.
One thing I find very helpful when writing instances for these classes is to explicitly write out what the type of each typeclass function is supposed to be, when applied to our type. For instance, the type of fmap would be:
fmap :: (a -> b) -> Logger a -> Logger bSince this is one of the most important exercises in the entire post, let's look at the solution a little more closely. The most important thing to notice is the definitions of (<*>) and (>>=). See how we're appending together the log messages that we got from unpacking each Logger at the end of each definition? That's the entire secret of how the final log output gets constructed.
Exercise 2: Since we're using monadic binds, we've abstracted over our log accumulator and don't have a convenient way to access it. So when we actually want to add a message, how do we do so? We could directly use the Logger constructor to add any messages that need to be added, as we did in the "ugly, but monadic" solution that we wrote above. But having to break open the internals of our abstraction just to write something so simple seems wrong. We can instead write a "primtive" Logger function to provide the functionality that's specific to our monad.
Define the function log:
log :: String -> Logger ()Exercise 3: As a convenience, it'd be nice to be able to log multiple messages at once.
Define the function logs:
logs :: [String] -> Logger ()Exercise 4: We now have everything we need. Rewrite the arithmetic functions from before using log, logs, and do-notation. Try running them and getting the log output.
If you've gotten this far, hopefully everything should be clicking into place.
You can skip this section if you feel like you understand how everything works sufficiently at this point.
Let's take one last look at how everything fits together. We've written all the individual pieces, but how does it all combine to produce something that "magically" combines all the output for us?
Initially we saw that we could get the behavior we wanted using nothing but pure functions and values. Here's where we circle back around and see that what we've written is also nothing but pure functions and values.
Now that we've done the implementation, reflect back on the "ugly-monadic" versions of our functions that we wrote before implementing.
addTwo :: Int -> Logger Int
addTwo x = Logger (["adding two..."], x + 2)
augmentAndStringify :: Int -> Int -> Logger String
augmentAndStringify x y =
Logger (["augmenting..."], ()) >>= (\_ ->
addTwo x >>= (\x' ->
addTwo y >>= (\y' ->
Logger (["stringifying..."], show (x' + y')))))With the hindsight of knowing what (>>=) is actually doing in our case, can you see how at each usage point, it's taking the tuples inside the Loggers on both sides, and doing the combining that previously we were doing manually?
We've successfully managed to get rid of a lot of boilerplate in our code. However, we're not quite done yet. Remember how we said that the type that we were working with wasn't as general as it could be yet? What we have right now solves the problem of logging messages, but it seems like this could be applied to a lot more situations. What if you want something more like an event log, where the messages are actual data structures? And it may not be obvious yet, but this same pattern can be used to do things like find minimums or check that a property holds while traversing a data structure. Surely we don't have to reimplement everything for similar, but slightly different problems?
Before, we also saw that (log, a) i.e. a completely generic tuple might be a valid type to try for our monad. But if we attempt to use that directly, we run into a bit of a problem. With Logger, our code gave us lots of values of type [String], and we know how to combine those pretty easily. But if the log type is completely abstract... how do we combine those? We don't know anything about them.
One idea might be to make the "log" output a list of our log type internally. For instance, you could think of something like this:
data Writer log a = Writer { runWriter :: ([log], a) }And that would work! But there's actually a better solution.
If we think about it, what we're actually looking for is to make it so our Writer can only be used with "combinable" values, ones where we can mash together smaller versions of the same type and produce something "bigger" of the same type. And as it turns out, there's already a name for those kinds of values: monoids!2 And just like things being equatable through Eq or comparable through Ord, Haskell conveniently lets you state that things are combinable through the Monoid typeclass. Lists are an instance of this typeclass, as are a bunch of other things.
Specifically, if something is a monoid, you get two functions you can use:
mappend :: Monoid a => a -> a -> alets you combine two values into a single one. For lists, this would be append.mempty :: Monoid a => agives you an "empty" value of that type, where combining this value with any other value gives you back the other value. For lists, this would be the empty list.
So what if we made our data definition like so:
data Writer log a = Writer { runWriter :: (log, a) }and only implemented our instances if the "log" type was a Monoid?
Exercise 5: Implement the Functor, Applicative, and Monad instances for our Writer type above.
Keep in mind that some instances may not need the Monoid constraint. Remember that you only need that constraint if you need to combine the "log" value.
Exercise 6: Go back and rewrite the "log a list of messages" function in terms of our new, more generic type.
Specifically, define the function tell:
tell :: log -> Writer log ()After you've implemented this, ask yourself: why don't you need a Monoid constraint on this function? Will our Writer still work without it?
Exercise 7: Rewrite log in terms of tell, using our Writer type instead of Logger.
Exercise 8: Rewrite the arithmetic functions from before using Writer instead of Logger, using our rewritten log function and do-notation.
If you've gotten to this point: congratulations! Presumably you get the point and understand how all this fits together after implementing it for all of State, Reader, and Writer. One last diagram to recap Writer thus far:

Bonus Exercise 1: Sometimes after calling some sub-function, we'd like to run some arbitrary function or transformation on the "log" output it gives us, rather than combining it immediately.
Define the function censor:
censor :: (log -> log) -> Writer log a -> Writer log aBonus Exercise 2: While we said initially that our output would be write-only, we can actually reclaim some small introspection capability. Notice how in the longhand prototype we initially wrote, we kept track of the output of each function we called. So if we wanted to branch off what our called functions gave us, technically we could. Can we get that visibility back?
Define a function listen:
listen :: Writer log a -> Writer log (a, log)At this point... you're done! Congratulations, because this can be one of the most challenging parts of learning Haskell. Do you feel more enlightened now?
There are a few extra points I'd like to call to your attention, though. Call them further insights you might have after going through this.
Firstly, what does making our Writer more general using Monoid actually buy us? I won't go into too much detail, but there are lots of different types that implement Monoid, and now all of them can be used inside our Writer. As previously mentioned, lists are one of these types, so you can accumulate lists of any type you want now. But other possible options are things like Min or All, to keep track of a minimum value or whether a property has held for everything you've seen thus far. And if you have your own data that seems "combinable" in this way, there's nothing stopping you from defining your own Monoid instances and using them with Writer as well.
Secondly, notice once again that the type that we ended up with is essentially just a tuple. And in fact, the Writer monad that we've implemented here is exactly the monad instance that's defined on 2-tuples! Try it out yourself and see. Unlike with Reader and functions, I don't think there's anything particularly elucidating to learn here about the structure of programming; it just happens to be one possible way to use tuples. Still, I personally think it's cool how the same fundamental pieces keep popping up over and over again when looking at the higher-level concepts.
To wrap up this series of posts:
- Monads in Haskell aren't anything special, they're just normal data structures that you can create yourself, and anything you could do with other values, you can do with monadic values. They just happen to often be useful for abstracting common patterns that come up when composing functions.
- At the end of the day, it's all just pure functions and values.
- There's nothing wrong with writing things out the longhand way, using only the simplest concepts in the language. It's up to you to decide whether you want to add complexity to abstract your code or not.
Again, just like our State implementation, DO NOT use this implementation for real code. It's correct, it will give you the same results as "real" Writers that you'll find in libraries, but using this in a real program will likely create performance problems and space leaks. Generally, Writer isn't used that commonly in the first place, compared to the other two monads in the RWS trifecta, but if you do find that it's a good fit for your situation, or if you just want to experiment, use an actual implementation from transformers.
And that wraps up the Writer monad. Are there other concepts in the Haskell ecosystem that you feel like you struggle with? Found this helpful, or otherwise have questions or comments? Talk to me!
Before you close that tab...
Want to become an expert at Haskell, but not sure how? I get it: it's an endless stream of inscrutable concepts and words, as if you've stepped into some strange bizarro world. Where do you even start? Why does any of this matter? How deep do these rabbit holes go?
I want to help. What if you always knew exactly what the next signpost on your journey was, if you always knew exactly what to learn next? That's why I created a Roadmap to Expert for you: a checklist of everything you need to know, sorted by difficulty, broken down into individual, easily-digestible chunks. Best of all: it's free! Just sign up for my email list below.
And there's more where that came from: Only a fraction of what I write ends up on this blog. Sign up and get advice, techniques, and templates for writing real, useful programs, straight to your inbox.
Absolutely no spam, ever. I respect your email privacy. Unsubscribe anytime.
Footnotes
↥1 Okay, so the actual signature you’d expect would probably be something like Num a => a -> a, but let’s keep it simple; Haskell’s numeric typeclass tower is not the focus here.
↥2 If you want to pedantic, fine, monoids describe a very specific kind of combining, with semigroups, groups, categories, etc. also all potentially fitting this description. Again, not the focus.